|
|
|
当前位置:首页 > 出版社书目索引 > 书目索引(按照出版时间先后顺序排序) 点击返回
-
-
-
- 初等数论
- 舒彦强, 段春华, 蒋太平主编/2022-8-1/
湖南大学出版社/定价:¥32
本选题根据师范教育的特点,尊重学生的基础,遵循学生的认知规律,适当降低理论要求。精选最基本、应用最广泛的知识内容。既体现数论逻辑严密性,又要结合学生专业特点和实际需求,把握好适合师范院校专科层次学生的学习难度:保留最基本的证明,删减难度较大的内容,适当加大应用性。全书共五章,详细介绍了数的基础、数的整除、同余、不定方程 -
ISBN:9787566726339
-
-
-
-
-
-
-
|

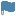 书单推荐
书单推荐 新书推荐
新书推荐